Electrophoretic Light Scattering - Overview

When an electric field is applied across an electrolytic solution, charged particles suspended in the electrolyte are attracted towards the electrode of opposite charge. Viscous forces acting on the particles tend to oppose this movement. When equilibrium is reached between these two opposing forces, the particles move with constant velocity. The magnitude of the velocity is dependent upon the strength of electric field or voltage gradient, the dielectric constant of the medium, the viscosity of the medium and the particle surface charge density

In electrophoretic light scattering (ELS), the velocity of a charged particle under the influence of an applied electric field is measured by monitoring the frequency shift (Dn) of the light scattered from the particle. Light scattered from stationary particles will have the same frequency and wavelength as the incident light, whereas light scattered from particles in motion will be Doppler shifted. In ELS, the velocity or mobility (U_e) of the particle is calculated from the Doppler frequency shift using the expression shown below, where q is the scattering angle and l is the wavelength of the incident light.

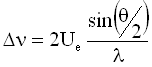
Doppler (Frequency) Shift

The intensity of a quantum of light is equivalent to the square of the wave amplitude. For 633 nm incident light, the frequency is 4.7 x 10¹⁴ Hz (= 1/s), which due to the sinusoidal behavior of the wave, yields an intensity frequency of twice this value. In modern light scattering instrumentation, the scattering intensity is monitored using an Avalanche Photo-Diode (APD) detector. The response time for an APD is on the order of 0.1 ms, which corresponds to 1 x 10⁷ Hz. As a consequence of this seven orders of magnitude difference between the light and detector response frequencies, an APD detector cannot be used to "directly" measure the frequency of the scattered light, much less the difference in frequencies between the incident and Doppler shifted light. Using a method called heterodyning however, the APD can be used to "indirectly" measure the frequency shift of the scattered light.

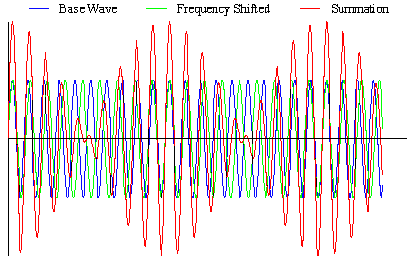
In the method of heterodyning, a fraction of the incident light is mixed with the scattered light to generate a "beat" pattern, the frequency of which can be easily monitored with a time dependent intensity trace from an APD. This method is most easily described using wave addition schematics. Consider for example, the figure below, which shows two waves of slightly different frequencies (Base Wave & Frequency Shifted), along with the Summation of the two. As shown in this schematic, the summation of the base and frequency shifted waves produces a wave, which pulses or "beats" at a lower frequency than either of the components.

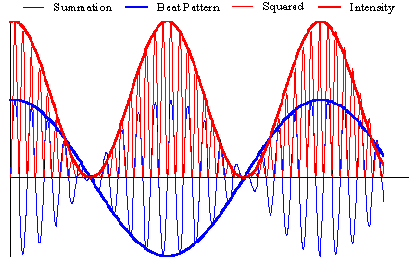
As noted earlier, the intensity is equivalent to the square of the amplitude. When the heterodyned wave is squared, the result is an oscillating intensity signal, which is easily measured with an APD and from which the beat frequency can be determined. Once the beat frequency is determined, the Doppler or frequency difference between the two component waves (photons), and the subsequent electrophoretic mobility (velocity) can be calculated.

Electrical Double Layer

The presence of a charge on the surface of a particle will influence the distribution of ions in the surrounding interfacial region. The result is an increased concentration of counter ions of opposite charge to that of the particle near the particle surface. As one moves away from the particle surface, the heterogeneous distribution of ions will eventually become homogeneous. The distance at which a homogenous distribution is obtained is called the Debye length (1/k) or screening distance, and is dependent upon the ionic strength as shown in the expression below, where e_o is the permittivity of free space (8.854 x 10^-12 F m^-1), e_r is the permittivity of the liquid, k is the Boltzmann constant (1.38 x 10^-23 J K^-1), T is the temperature in Kelvin, e is the electronic charge (1.6022 x 10^-19 C), I is the molar ionic strength, and N_A is Avogadro’s constant (6.022 x 10²³ mol^-1).

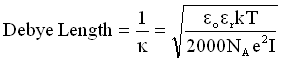
The molar ionic strength can be calculated from the following equation, where C_i is the ionic species concentration and Z_i is the valency.

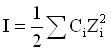
For water at 298 K, the Debye length expression reduces to the following form.

The liquid layer surrounding the particle exists as two parts; an inner region (Stern layer) where the ions are strongly bound and an outer (diffuse) region where they are less firmly associated. Within the diffuse layer there is a notional boundary inside which the ions and particles form a stable entity. When a particle moves, ions within this boundary move with it. Those ions beyond the boundary do not travel with the particle. The electric potential at this boundary, also called the surface of hydrodynamic shear, is defined as the zeta potential.

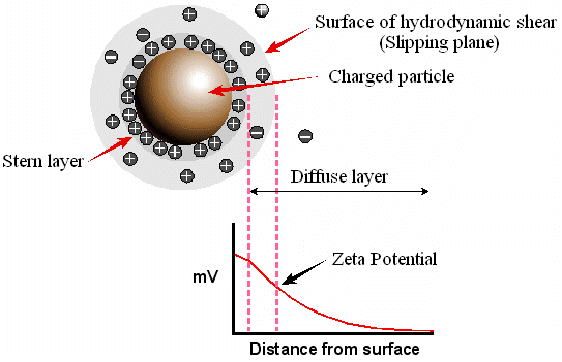
Zeta Potential

The magnitude of the zeta potential gives an indication of the electrostatic stability of the colloidal system. If all the particles in suspension have a large negative or positive zeta potential, then they will tend to repel each other and there is no tendency for the particles to come together. However, if the particles have low zeta potential values, then the electrostatic force is insufficient to prevent the particles from coming together and aggregating or flocculating. The rule of thumb dividing line between electrostatically stable and unstable suspensions is generally taken at either +30 or -30 mV. Particle/dispersant systems with zeta potentials more positive than +30 mV or more negative than -30 mV are normally considered electrostatically stable.

In electrophoretic light scattering, the zeta potential (z) is calculated from the measured electrophoretic mobility (U_e) using the Henry equation shown below, where e is the dielectric constant, h is the solution viscosity, k is the inverse Debye length, a is the particle radius, and f(ka) is the Henry function.

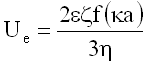
The units of k are reciprocal length, with 1/k being the "thickness" of the electrical double layer (Debye length). The parameter a refers to the radius of the particle, and therefore, ka is the ratio of the particle radius to the electrical double layer thickness. The Henry function, f(ka), in the expression above ranges from 1 (Huckel limit) to 1.5 (Smoluchowski limit).

Henry Function

In the expression for electrophoretic mobility and zeta potential, the Henry function is a scalar, and describes the retardation of the mobility arising from the presence of the ionic atmosphere. For a sphere in the presence of mobile ions, the Henry function is defined as shown below.

For ka > 1

For ka < 1

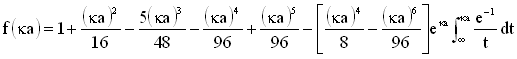
The limiting conditions for the Henry function are represented schematically in the figure below. Under conditions where the Debye length is small compared to the particle radius, Henry’s function reduces to the Smoluchowski limit of 1.5. For conditions where the particle radius is small compared to the Debye length, Henry’s function reduces to the Huckel limit of 1.

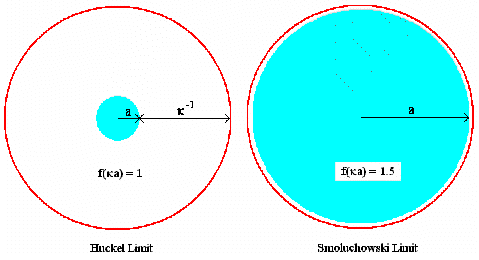
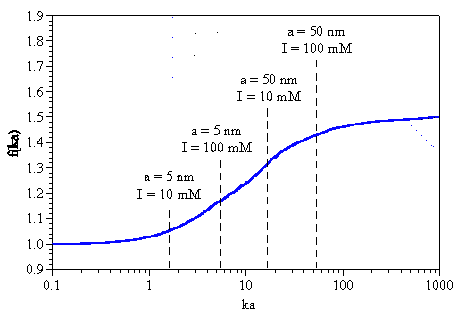
For a given combination of particle size and solution ionic strength, the Henry function can be used to calculate the appropriate f(ka) value for use in a zeta potential measurement. The figure below shows a graphical representation of the Henry function, along with the ka values for four particle size and ionic strength combinations. Electrophoretic determinations of zeta potential are most commonly made in aqueous media at moderate electrolyte concentration. As seen in the figure below, the Smoluchowski limit of f(ka) = 1.5 is appropriate for larger particles and colloids under ionic strength conditions of ³ 10 mM. For small particles such as proteins in a low dielectric (or low ionic strength) medium, the Huckel limit of f(ka) = 1 is the more appropriate model.

It should be noted here, that the accuracy of the Henry function for the calculation of the zeta potential falls off for |z| > 25 mV. For larger zeta potential values, the fuller treatment of the balance between viscous and electrophoretic forces provided in the O’Brien-White, or more recently the White-Mangelsdorf theory is more appropriate.

Particle/Dispersant Pairs

As discussed earlier, the zeta potential is the electrostatic potential measured at the slipping plane or plane of hydrodynamic shear. The summation of charges within this boundary would include the particle valence charge, the charge arising from condensed (surfaced absorbed) counterions, and the charge from any non-absorbed associated ions diffusing with the particle. All of these sources of charge will have an influence on the magnitude of the measured zeta potential at the slipping plane. As such, it is meaningless to report a zeta potential value for a particle, in the absence of a description of the dispersant conditions, e.g. pH, ionic strength, additive concentrations, etc.

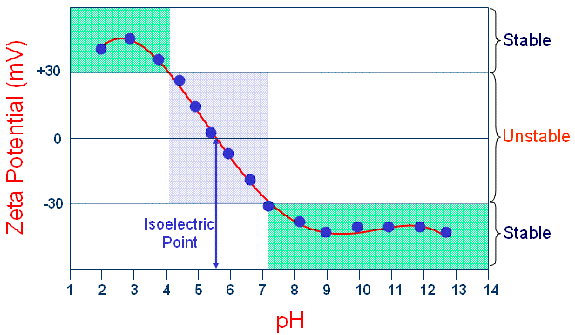
One of the most important factors influencing zeta potential is pH. Consider for example, a particle in suspension with a positive zeta potential. As base is added to the solution, the pH will increase, as will the concentration of hydroxide ions (OH^-), which will tend to neutralize the positive charges on the particle surface. Ergo, one would expect and observe, a decrease in the zeta potential as base is added to the solution. If sufficient base is added to the system, the summation of charge within the slipping plane boundary may very well go to zero, resulting in a zero electrophoretic mobility. The pH at which this condition arises is defined as the isoelectric point, e.g. the pH at which the electrophoretic mobility is zero. From a practical consideration, the isoelectric point also happens to be the point of least electrostatic stability for a colloidal system. Depending upon the type of valence residues on the particle surface, further addition of base to the original solution may lead to a reversal of the sign and a negative zeta potential. A typical isoelectric titration plot for a protein sample is shown in the figure below. As noted in this figure, the isoelectric point of this protein is circa 5.5, with the pH regions of electrostatic stability being pH < 4 and pH > 7.2.

For additional questions or information regarding Malvern Instruments complete line of particle and materials characterization products, visit us at www.malvern.com.