

In typical dynamic light scattering (DLS) instrumentation, there is a single detector fixed at a single angle. The measured data in a DLS experiment is the intensity autocorrelation curve. Embodied within the autocorrelation curve is all of the information regarding the size distribution of the ensemble collection of particles in the solution. Deconvolution of the intensity autocorrelation curve to an intensity distribution is an ill defined problem. As such, there is an inherent degree of uncertainty in DLS derived intensity size distributions. This inherent uncertainty translates into peak broadening or an apparent in the width of the intensity distribution. For typical laboratory samples, this increase can amount to as much as a 10 – 15%. When Mie theory (or any other volume vs size algorithm) is applied to the DLS intensity distribution, the algorithm cannot distinguish this apparent increase in width from the true width. As such, all of the "size bins" in the intensity distribution are treated as though they are real, i.e. a fraction of the sample that has a slightly different size from that of the mean (see schematic shown in Figure 1).
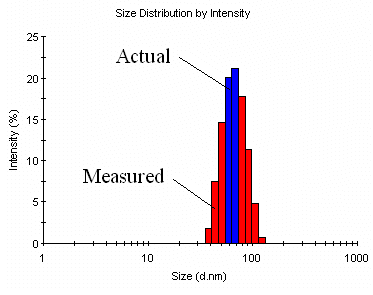
Figure 1: Schematic showing a comparison of a DLS measured intensity distribution to the number distribution for a 62 nm latex.
As a consequence of the peak broadening inherent to DLS measurements, volume or mass distributions derived from DLS based intensity distributions are skewed towards smaller sizes. Consider for example the distributions shown in Figure 2. The dashed line in Figure 2 represents the true size of the monodisperse sample and is consistent with the mean of the intensity distribution. The volume distribution on the other hand, gives a mean value that is smaller than the true value.
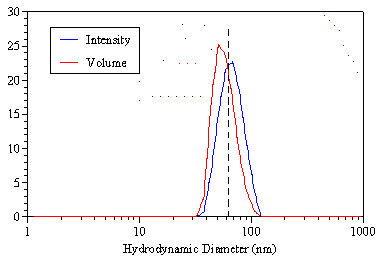
Figure 2: Comparison of the DLS intensity and volume distributions for a latex standard with a 62 nm hydrodynamic diameter.
A more appropriate use of DLS derived volume distributions is in the area of sample composition. The sample scattering intensity is proportional to the square of the molecular weight (or ~ R6, where R is the radius). As a consequence, a small amount of large particles can appear to dominate the DLS measured intensity distribution. The molecular weight squared effect can be normalized however, by transformation of the intensity distribution into a mass distribution. Consider Figure 3 for example, which shows the DLS derived intensity and volume distributions for an equal mass mixture of 62 and 220 nm latex spheres. The appropriate sizes to report are those from the intensity distribution (table inset). The area under each peak is proportional to the relative amount of each particle family. By intensity, 88% of the distribution contribution is from the larger 220 nm particles. The mass distribution however, is much more consistent with the known equal mass composition, with 53% of the mass attributed to the larger particle and 47% attributed to the smaller particle.
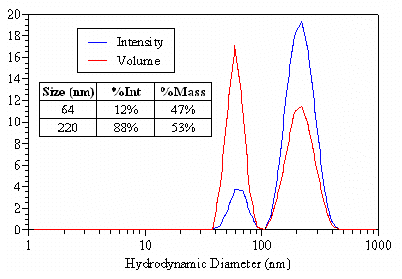
Figure 3: Comparison of the DLS derived intensity and volume distributions for an equal mass mixture of 62 and 220 nm latex spheres, along with the %composition results.
For additional questions or information regarding Malvern Instruments complete line of particle and materials characterization products, visit us at www.malvern.com.
