

Light scattering arises from the interaction of light with matter. When light interacts with an isolated molecule, the oscillating electromagnetic wave induces a dipole in the molecule that oscillates with the same frequency as the incident light. Characteristic of an oscillating dipole is ‘acceleration of charge.’ When a charge is accelerated, energy is emitted in all directions within a plane perpendicular to the line of acceleration. It is the energy emitted from the oscillating dipole, induced by the interaction of the incident light with the molecule, that is referred to as scattered light. The frequency of the scattered light is equivalent to the oscillation frequency in the induced dipole, which is equivalent to the frequency of the incident light. Hence the frequency of the scattered light is the same as that of the incident beam.
For small particles and plane polarized incident light, the scattering intensity is equal in all directions within the planes perpendicular to the polarization plane. The scattering intensity is maximum in the perpendicular plane containing the scattering center, but is zero along the axis of oscillation of the induced dipole. The scattering profile can be visualized then, by centering the origin on the scattering molecule, with the X axis aligned with the direction of propagation of the incident light, and rotating a ‘figure eight shape’ around the axis of oscillation. The figure below shows a representation of the scattering profile for vertically polarized incident light. The scattering angle (q) is defined as the angle between the transmitted light axis (X) and the detector located in the XY plane. As indicated in this figure, the scattering intensity from a small isolated molecule is the same for all q if the incident light is vertically polarized.
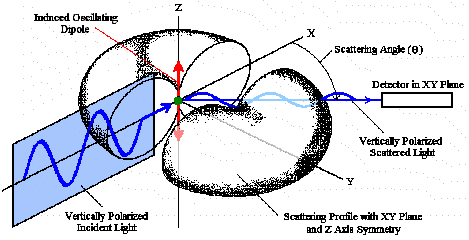
For horizontally polarized incident light, the axis of oscillation of the induced dipole is along the Y axis. The ‘doughnut’ shaped scattering profile then is visualized by rotating the figure eight around the Y axis. Since the detector is still located in the XY plane however, the intensity from horizontally polarized incident light is dependent upon the scattering angle, being maximized at q = 0 and zero at q = 90. Non-polarized light contains both horizontal and vertical components, with the scattering profile being a sum of the profiles arising from the two components.
For particles much smaller than the wavelength of the incident light, the assumption that the particle interacts with only a single photon is valid. As the particle increases in size, the likelihood of multiple photons striking the same particle also increases. Multiple photons interacting with the same isolated particle will induce multiple dipoles. The scattering intensity monitored at a fixed position detector will be the sum of the intensities generated from each of these dipoles. As a consequence of constructive and destructive interference then, the scattering intensity from a large isolated molecule is dependent upon the location of the detector, i.e. the scattering angle.
The Rayleigh expression used to describe the light scattered from a dilute solution of particles can be written as shown below, where K is an optical constant, C is the particle concentration, Rq is the Rayleigh ratio of scattered to incident light intensity, M is the weight average particle molecular weight, A2 is the 2nd virial coefficient (representative of inter-particle interaction strength), Rg is the particle radius of gyration, lo is the vacuum wavelength of the incident light, q is the scattering angle, NA is Avogadro’s number, ño is the solvent refractive index, and dñ/dC is the solvent dependent refractive index increment for the analyte.
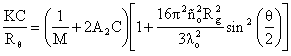
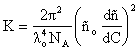
The angular dependent portion of the second term in the Rayleigh expression arises from interference effects due to multiple scattering from a single particle. For particles much smaller than the wavelength of the incident radiation, this term goes to zero, and the angular dependence of the scattered light vanishes. Under these conditions, the Rayleigh expression can be simplified to the form shown below, and the molecular weight can be determined from the concentration dependence of the Rayleigh ratio using single angle light scattering, i.e. a plot of KC/Rq vs. C, with the molecular weight determined from the intercept and the 2nd virial coefficient determined from the slope.
![]()
For larger particles, it is still the concentration dependence that is typically used to determine the molecular weight, but interference effects must be accounted for. It is at this point that multi-angle instruments become necessary. As a rule of thumb, the size cutoff for angle independent Rayleigh scattering is Rg £ l/20. The radius of gyration (Rg) is a mass average radius. For globular particles such as proteins, the hydrodynamic radius (RH) measured by dynamic light scattering techniques, is roughly equivalent to the radius of rotation about the center of mass + the thickness of a single layer of solvent. For globular proteins, Rg is ~25% smaller than RH. By comparison then, the Rg £ l/20 cutoff is consistent with a hydrodynamic diameter of ~ 80 nm for globular type molecules such as proteins.
For small particles, molecular weight measurements can be performed using the single angle form of the Rayleigh equation for small particle scattering shown above. The Rayleigh ratio for each intensity reading is calculated according to the expression shown below, where IA is the residual intensity of the analyte, IT is the toluene intensity, ñT is the toluene refractive index, ño is the solvent refractive index, and RT is the Rayleigh ratio for toluene.
![]()
The residual intensity is calculated according to the expression given below, where Intensity is the measured intensity of the sample and Solv Int is the intensity of the solvent.
Res Int = Intensity – Solv Int
The wavelength and temperature dependent toluene refractive index is calculated according to the expression shown below, where T is the temperature (C) and lo is the vacuum wavelength (nm) of the incident light.
![]()
The wavelength dependent Rayleigh ratio for toluene is calculated according to the expression shown below, where lo is the vacuum wavelength (nm) of the incident light.
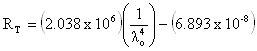
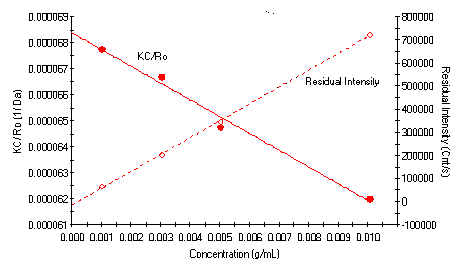
A Debye plot is a linear fit of KC/Rq vs. concentration, where the intercept is equal to the inverse of the molecular weight and the slope is proportional to the 2nd virial coefficient. An example of a Debye plot for lysozyme in phosphate buffered saline at pH 6.8 is given below. From the intercept, the measured MW is 14.6 kDa, consistent with the know value of 14.7 kDa. From the slope, the 2nd virial coefficient for this protein/solvent pair is –3.229 x 10-4 mL mol / g2.
For additional questions or information regarding Malvern Instruments complete line of particle and materials characterization products, visit us at www.malvern.com.
