What does polydispersity mean?

The term polydispersity has multiple meanings that are dependent upon the context of its use. In the area of polymer chemistry, polydispersity is defined as the weight average divided by the number average molecular weight (M_w/M_n), and is used to give the researcher an idea of the breadth or width of the molecular weight distribution. In a similar albeit not identical sense, polydispersity in the area of light scattering is used to describe the width of the particle size distribution.

In the light scattering area, the term polydispersity is derived from the polydispersity index, a parameter calculated from a Cumulants analysis of the DLS measured intensity autocorrelation function. In the Cumulants analysis, a single particle size is assumed and a single exponential fit is applied to the autocorrelation function. The autocorrelation function, along with the exponential fitting expression, is shown below, where I is the scattering intensity, t is the initial time, t is the delay time, A is the amplitude or intercept of the correlation function, B is the baseline, D is the diffusion coefficient, q is the scattering vector, l_o is the vacuum laser wavelength, ñ is the medium refractive index, q is the scattering angle, k is the Boltzmann constant, T is the absolute temperature, h is the viscosity of the medium, and R_H is the hydrodynamic radius.

In the Cumulants approach, the exponential fitting expression is expanded to account for polydispersity or peak broadening effects, as shown below.

The expression is then linearized and the data fit to the form shown below, where the D subscript notation is used to indicate diameter. The 1^st Cumulant or moment (a₁) is used to calculate the intensity weighted Z average mean size and the 2^nd moment (a₂) is used to calculate a parameter defined as the polydispersity index (PdI).

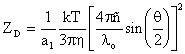
It is important to note here, that the Cumulants analysis algorithm does not yield a distribution – it gives only the intensity weighted Z average and the polydispersity index. If one were to assume a single size population following a Gaussian distribution, then the polydispersity index would be related to the standard deviation (s) of the hypothetical Gaussian distribution in the fashion shown below.

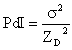
Using the above expression, polydispersity can then be defined in the following terms.

Polydispersity Index (PdI) = Relative variance

Polydispersity (Pd) = Standard deviation or width¹

%Polydispersity (%Pd) = Coefficient of variation² = (PdI)^½ x 100

¹ Also known as the absolute polydispersity

² Also called the relative polydispersity

Of the three terms defined above, the coefficient of variation or %Pd is one of the more often used parameters in the area of protein analysis. The fitting of the measured autocorrelation function is an ill-posed problem. Which means that there are multiple distributions that can be transformed from the correlogram, depending upon how much noise is assumed. Because of the inherent uncertainty arising from this problem, DLS derived size distributions will always have a small degree of polydispersity, even if the sample consists of a very monodisperse analyte. As a rule of thumb, samples with %Pd < ~ 20% are considered to be monodisperse.

While the above terms were derived from a Cumulants parameter (PdI), they are also routinely used to describe individual peaks in particle size distributions derived from multi-modal (or multi-peak) correlogram fitting algorithms such as CONTIN and NNLS (non-negative least squares). Consider for example, the distribution and Cumulants results shown in Figure 1, collected with a Malvern Zetasizer Nano system. The single mode Cumulant results indicate an intensity weighted Z average size of 157 nm with a polydispersity index of 0.222. If one were to assume a single particle family with a Gaussian distribution (represented by the monomodal distribution in Figure 1), the relative standard deviation or %Polydispersity (%Pd) for this hypothetical Gaussian would be 47%, suggesting a wide distribution. In reality, the sample is composed of a mixture of 60 and 200 nm latex size standards, as verified by the distribution results derived from an NNLS analysis of the correlogram, which indicate narrow or low polydispersity for both particle families.

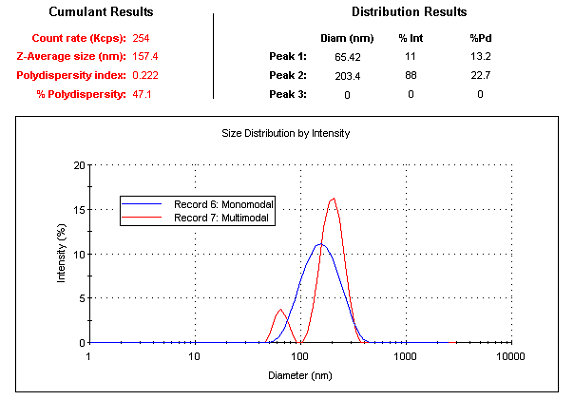
Figure 1: Cumulant and NNLS results for a mixture of 60 and 200 nm latex size standards measured with a Malvern Zetasizer Nano system.

For additional questions or information regarding Malvern Instruments complete line of particle and materials characterization products, visit us at www.malvern.com.