

A common dilemma in the area of light scattering based sizing measurements of concentrated samples is the question of whether or not the results are free of particle interaction effects. One aspect of the "particle interactions" category is the hydrodynamic effect, also known as restricted or hindered diffusion. Restricted diffusion refers to the phenomenon wherein the particle translational diffusion coefficient is reduced, not due to an increase in particle size, but rather due to a reduction in the free space within which the particle can diffuse.
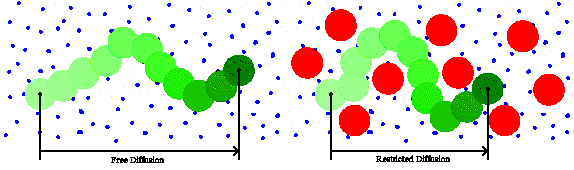
Figure 1: Schematic describing the effect of restricted diffusion at high sample concentration on the measured translational diffusion coefficient.
In a dynamic light scattering measurement, the solution property that is measured is the translational diffusion coefficient, or more specifically, the distribution of diffusion coefficients. The transformation of the diffusion coefficient distribution to the particle size distribution is accomplished using the Stokes-Einstein equation shown below, where RH is the hydrodynamic radius, k is the Boltzmann constant, T is the temperature, D is the diffusion coefficient, and h is the viscosity of the medium.
![]()
Under classical dilute concentration light scattering conditions, the accepted viscosity value for use in the above expression is that of the solvent or dispersant. Modern light scattering instruments such as the Zetasizer Nano system however, can accommodate sizing measurements at high sample concentration. Under these higher sample concentration conditions, the viscosity of the bulk solution rather than the dispersant viscosity is considered to be the more appropriate viscosity parameter for use in the Stokes-Einstein transform, particularly if the sample exhibits Newtonian fluid characteristics.
In dynamic light scattering, restricted diffusion effects are typically manifested as an increase in the apparent particle size, with no significant change in the polydispersity (or width) of the distribution. Consider Figure 2 for example, which shows the concentration dependence of the measured size distribution for a flavored alcoholic beverage emulsion. For all of the measurements displayed in this figure, the viscosity of the diluent (water) was used for the Stokes-Einstein calculation. As seen here, in increase in sample concentration leads to an apparent increase in particle size, with no noticeable change in the width of the distribution, suggesting the influence of restricted diffusion effects.
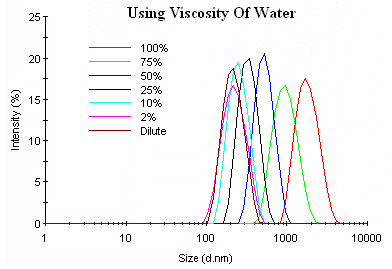
Figure 2: Concentration dependence of the measured particle size distribution for a flavored alcoholic beverage emulsion, using the viscosity of the diluent (water) in the Stokes-Einstein calculation.
A comparison of the Z average diameter to the dynamic viscosity of the bulk solution for the same emulsion sample is shown in Figure 3. As seen in this figure, the concentration dependence of the apparent Z average size (¢) parallels the concentration dependence of the dynamic viscosity (p), when water (solvent or diluent) is used in the Stokes-Einstein calculation. Compensation for restricted diffusion effects is achieved when the dynamic viscosity is used in the Stokes-Einstein transform, yielding a Z average size (˜) that is independent of sample concentration.
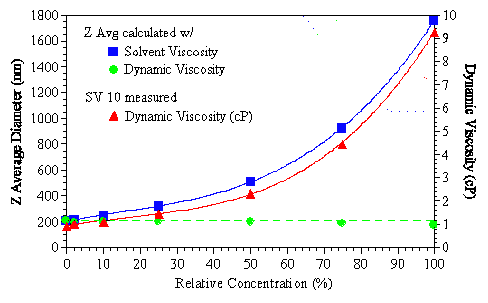
Figure 3: Comparison of the concentration dependence of the viscosity (p) of the bulk sample to the Z average diameter calculated using the viscosity of the water diluent (¢) and the viscosity of the bulk sample (˜).
Figure 4 shows the concentration dependent size distributions from Figure 2, recalculated using the viscosity of the bulk sample to compensate for restricted diffusion effects. As with the Z average diameter, the use of the bulk sample viscosity virtually eliminates the concentration dependence, yielding a size of circa 200 nm for all sample concentrations.
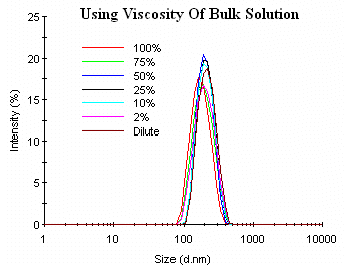
Figure 4: Concentration dependent size distributions from Figure 2, recalculated using the viscosity of the bulk sample to compensate for restricted diffusion effects.
While the dynamic light scattering results for the emulsion presented in this FAQ appear to be conclusive with regard to using the viscosity of the bulk sample to compensate for restricted diffusion effects, it must be recognized that this is an ideal Newtonian fluid sample. The "particle interactions" classification is the Gideon’s Knot of light scattering experiments, and many times, restricted diffusion effects are accompanied by other types of particle interactions including hard particle and electrostatic effects. For this reason, it is always good practice to examine the effects of dilution when attempting to measure particle size distributions of concentrated samples.
For additional questions or information regarding Malvern Instruments complete line of particle and materials characterization products, visit us at www.malvern.com.
