

When an electric field is applied across an electrolyte, charged particles suspended in the electrolyte are attracted towards the electrode of opposite charge. Viscous forces acting on the particles tend to oppose this movement. When equilibrium is reached between these two opposing forces, the particles move with constant velocity. The velocity is dependent on the strength of electric field or voltage gradient, the dielectric constant of the medium, the viscosity of the medium, and the zeta potential.
The velocity of a particle in a unit electric field is referred to as its electrophoretic mobility. The zeta potential is related to the electrophoretic mobility by the Henry equation shown below, where z is the zeta potential, Ue is the electrophoretic mobility, e is the dielectric constant, h is the viscosity of the dispersant, and f(ka) is the Henry function.
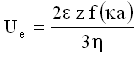
The units of k are reciprocal length. 1/k, also known as the Debye length, is defined as the scale over which mobile ions in the solution will screen an electric field. Put another way, the Debye length is the distance from the surface of a charged particle over which the electric field from the particle will affect the distribution of free ions in the solution. The Debye length is often taken as a measure of the "thickness" of the electrical double layer. The parameter "a" refers to the radius of the particle, and therefore ka is a measure of the ratio of the particle radius to the Debye length (or double layer thickness).
The Debye length can be calculated using the expression given below, where eo is permittivity of free space (= 8.854 x 10-12 F m-1), er is the dielectric constant, k is the Boltzmann constant (= 1.38 x 10-23 J K-1), T is the temperature in Kelvin, e is the electronic charge (= 1.6022 x 10-19 C), I is the ionic strength in molarity, and NA is Avogadros number (= 6.022 x 1023 mol-1).
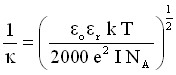
The ionic strength (I) in molarity can be calculated from the following equation, where Ci is the ionic species concentration and Zi is the valency.
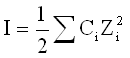
For water at 298 K, the Debye length expression reduces to the following form, where the units of k-1 are nm.
![]()
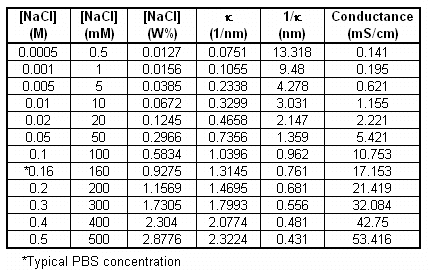
The dependence of the Debye length on the concentration of the monovalent salt, NaCl, can be seen in the following table. As expected, as increase in salt concentration leads to an increase in ionic shielding, and a subsequent decrease in the Debye length or double layer thickness.
The f(ka) term in the Henry equation is known as the Henry function, and for a sphere in the presence of mobile ions is defined as shown below.
For ka > 1
![]()
For ka < 1
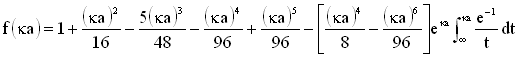
The limiting conditions for the Henry function are represented schematically in Figure 1. Under conditions where the Debye length is small compared to the particle radius, Henry’s function reduces to the Smoluchowski limit of 1.5. For conditions where the particle radius is small compared to the Debye length, Henry’s function reduces to the Huckel limit of 1.
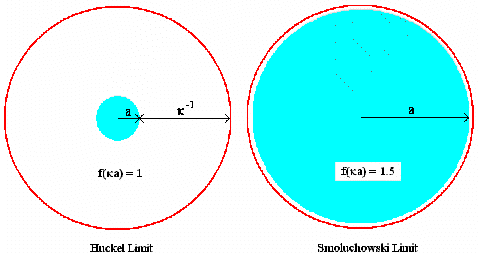
Figure 1: Schematics describing the Huckel and Smoluchowski limits of the Henry function, where "a" is the particle radius and k-1 is the Debye length or double layer thickness.
For a given combination of particle size and solution ionic strength, the Henry function can be used to calculate the appropriate f(ka) value for use in a zeta potential measurement. Figure 2 shows a graphical representation of the Henry function, along with the ka values for four particle size and ionic strength combinations. Electrophoretic determinations of zeta potential are most commonly made in aqueous media at moderate electrolyte concentration. As seen in Figure 2, the Smoluchowski limit of f(ka) = 1.5 is appropriate for larger particles and colloids under ionic strength conditions of ³ 10 mM. For small particles such as proteins in a low dielectric (or low ionic strength) medium, the Huckel limit of f(ka) = 1 is the better model.
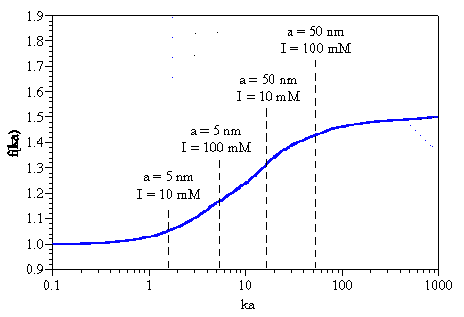
Figure 2: Graphical representation of the Henry function and the ka values for four example particle size and ionic strength combinations.
It is noted here in closing, that the accuracy of the Henry function for the calculation of the zeta potential falls off for |z| > 25 mV. For larger zeta potential values, the fuller treatment of the balance between viscous and electrophoretic forces provided in the O’Brien-White, or more recently the White-Mangelsdorf theory is more appropriate.
For additional questions or information regarding Malvern Instruments complete line of particle and materials characterization products, visit us at www.malvern.com.
